Поиск
| Автор | Сообщение |
|---|---|
|
Елена
#
3 янв 2007 |
|
|
Елена
#
3 янв 2007 |
|
|
О.А.
#
3 янв 2007 |
|
|
Елена
#
3 янв 2007 |
|
|
О.А.
#
3 янв 2007 |
|
|
Елена
#
3 янв 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
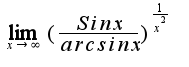 Неопределенность
Неопределенность 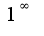 Очень уж смахивает на единицу, а получиться должен ноль... Подскажите, пожалуйста - через что решать...
Очень уж смахивает на единицу, а получиться должен ноль... Подскажите, пожалуйста - через что решать...
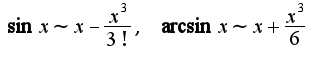 при
при 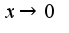
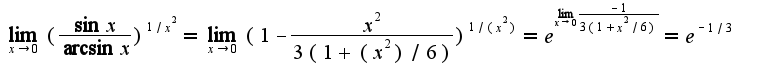
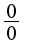 поэтому лучший метод решения, по-моему, использование замены эквивалентных или разложение функций в ряд.
поэтому лучший метод решения, по-моему, использование замены эквивалентных или разложение функций в ряд.