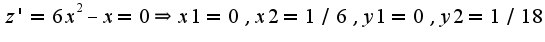Поиск
| Автор | Сообщение |
|---|---|
|
Sonya
#
17 ноя 2008 |
|
|
О.А.
#
17 ноя 2008 |
|
|
Sonya
#
17 ноя 2008 |
|
|
О.А.
#
17 ноя 2008 |
|
|
Sonya
#
18 ноя 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
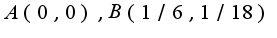 обе точки дают экстремум, в чем легко убедиться используя аппарат дифференциального исчисления
обе точки дают экстремум, в чем легко убедиться используя аппарат дифференциального исчисления
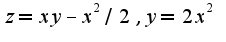 , получим
, получим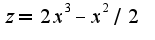 , находим производную по переменной
, находим производную по переменной  ,
,