Поиск
| Автор | Сообщение |
|---|---|
|
2131
#
17 фев 2006 |
|
|
О.А.
#
17 фев 2006 |
|
|
2131
#
24 фев 2006 |
|
|
О.А.
#
24 фев 2006 |
|
|
Любопытный человек
#
3 мар 2006 |
|
|
О.А.
#
4 мар 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
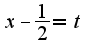 ;
2)
;
2)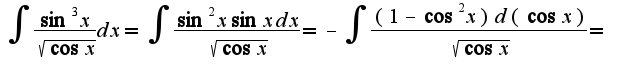
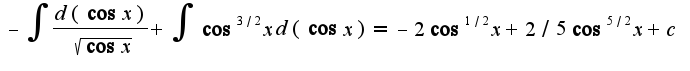 ;
3)в данном примере нужно сделать замену переменной
;
3)в данном примере нужно сделать замену переменной 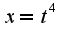 ;
4)
;
4)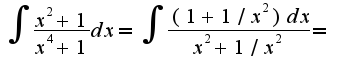
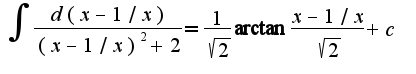
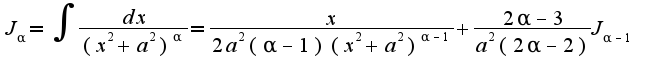 Поэтому
Поэтому 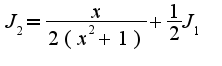 Здесь
Здесь 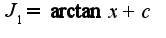
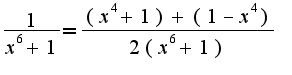
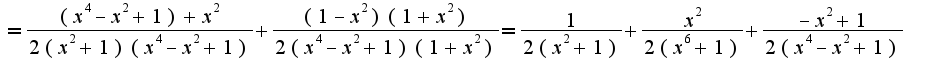 Данные первые два слагаемых легко проинтегрировать, последнее слагаемое надо разложить на простые дроби:
Данные первые два слагаемых легко проинтегрировать, последнее слагаемое надо разложить на простые дроби: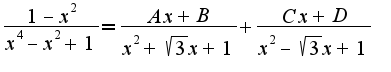 Легко найти коэффициенты:
Легко найти коэффициенты: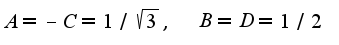 Окончательно,
Окончательно, 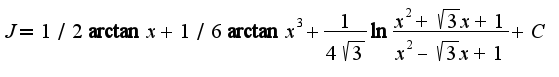 2)В данном примере либо разлагают на сумму пяти дробей
2)В данном примере либо разлагают на сумму пяти дробей 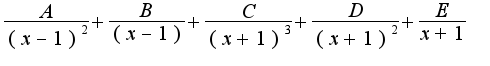 , либо применяют метод Остроградского (Ляшко И.И. и др. Математический анализ. К.,ч.1, с.381.)
, либо применяют метод Остроградского (Ляшко И.И. и др. Математический анализ. К.,ч.1, с.381.)