| Автор | Сообщение |
|---|---|
|
Mordecai
#
20 янв 2013 |
|
|
o_a
#
20 янв 2013 |
|
|
Кристи
#
17 апр 2013 |
|
|
o_a
#
17 апр 2013 |
|
|
Кристи
#
18 апр 2013 o_a
18 апр 2013
|
|
|
крас
#
16 мая 2013 |
|
|
Артем
#
18 мая 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
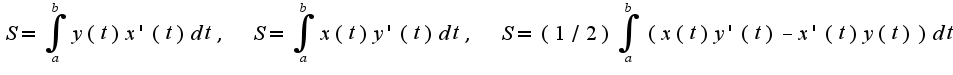 Используя первую из них, получим
Используя первую из них, получим