Поиск
| Автор | Сообщение |
|---|---|
|
Катя
#
11 фев 2005 |
|
|
О.А.
#
11 фев 2005 |
|
|
Катя
#
23 мая 2006 |
|
|
Ленка Фил
#
21 ноя 2006 |
|
|
О.А.
#
21 ноя 2006 |
|
|
Ленка Фил
#
21 ноя 2006 |
|
|
О.А.
#
21 ноя 2006 |
|
|
Ленка Фил
#
21 ноя 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
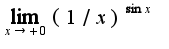
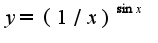 . Затем прологарифмируем данное выражение, получим:
. Затем прологарифмируем данное выражение, получим: 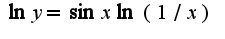 . Теперь найдем
. Теперь найдем 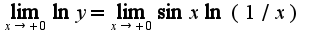 (неопределенность вида
(неопределенность вида 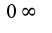 ). Преобразуем к неопределенности вида
). Преобразуем к неопределенности вида 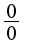 и применим правило Лопиталя:
и применим правило Лопиталя: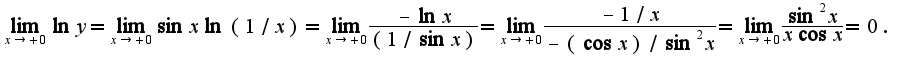 Таким образом,
Таким образом, 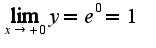 .
.
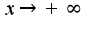 , то
, то 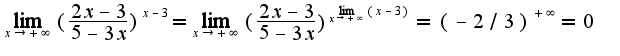 Если
Если 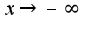 , то
, то 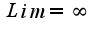 2)
2)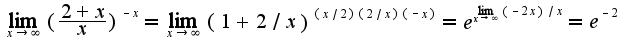 4)
4)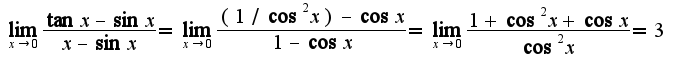
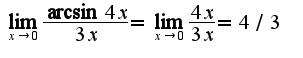 Т.к. известно асимптотическое равенство
Т.к. известно асимптотическое равенство 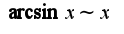 при
при 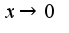 2)
2)