Поиск
| Автор | Сообщение |
|---|---|
|
ККК
#
20 янв 2009 |
|
|
О.А.
#
23 янв 2009 |
|
|
ККК
#
20 янв 2009 |
|
|
ККК
#
18 дек 2009 |
|
|
О.А.
#
20 янв 2009 |
|
|
ККК
#
20 янв 2009 |
|
|
О.А.
#
20 янв 2009 |
|
|
ККК
#
20 янв 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
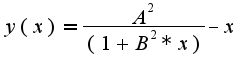 . Нужно найти ее максимум.
Первая производная:
. Нужно найти ее максимум.
Первая производная: 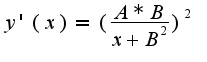 Я нашла критические точки, их две
Я нашла критические точки, их две 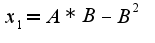 и
и 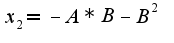 .
Решения получаются в виде формул, где
.
Решения получаются в виде формул, где 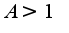 и
и 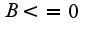 .
Поэтому я не могу проверить поведение функции справа и слева от этих точек.
Вторая производная:
.
Поэтому я не могу проверить поведение функции справа и слева от этих точек.
Вторая производная: 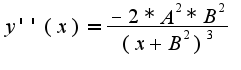 Видно, что она при любом
Видно, что она при любом  будет отрицательной.
Тогда какая из двух критических точек будет максимумом?
Что-то я запуталась...
Заранее спасибо!
будет отрицательной.
Тогда какая из двух критических точек будет максимумом?
Что-то я запуталась...
Заранее спасибо!
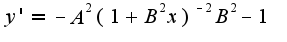
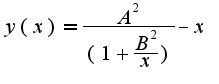 .
Нужно найти ее максимум.
Первая производная:
.
Нужно найти ее максимум.
Первая производная: 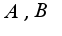
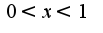 Поэтому и получается, что вторая производная всегда отрицательна.
А в первой производной я, наверное, когда ее сюда вписывала, ошибку сделала.
Поэтому и получается, что вторая производная всегда отрицательна.
А в первой производной я, наверное, когда ее сюда вписывала, ошибку сделала.