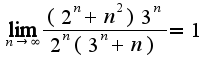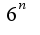Поиск
| Автор | Сообщение |
|---|---|
|
Паштет
#
7 июн 2009 |
|
|
О.А.
#
7 июн 2009 |
|
|
Паштет
#
8 июн 2009 |
|
|
О.А.
#
8 июн 2009 |
|
|
Паштет
#
8 июн 2009 |
|
|
О.А.
#
8 июн 2009 |
|
|
Паштет
#
9 июн 2009 |
|
|
О.А.
#
9 июн 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
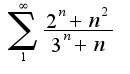 Заранее спасибо.
Заранее спасибо.
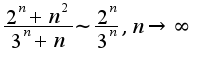
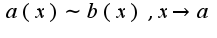 если
если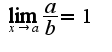 Если ряд
Если ряд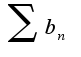 -сходится, то и ряд
-сходится, то и ряд 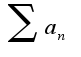 -сходится
-сходится
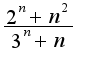 таки НЕ эквивалентно
таки НЕ эквивалентно 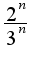 , я гарантирую это!
, я гарантирую это!