Поиск
| Автор | Сообщение |
|---|---|
|
Олег
#
11 дек 2007 |
|
|
О.А.
#
11 дек 2007 |
|
|
Олег
#
11 дек 2007 |
|
|
О.А.
#
11 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
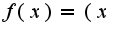 при
при 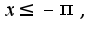
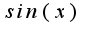 при
при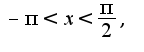
 при
при 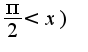 1) В точке (
1) В точке (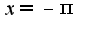 ) получается разрыв 1го рода, но условие выполняется не полностью (левый и правый пределы существуют и не равны, и _не равны значению функции в точке_). Левый предел =
) получается разрыв 1го рода, но условие выполняется не полностью (левый и правый пределы существуют и не равны, и _не равны значению функции в точке_). Левый предел =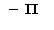 , правый
, правый 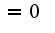 , функция в точке
, функция в точке 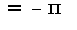 2) Вторая точка (
2) Вторая точка (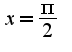 ). Устранимый разрыв? Левый и правый пределы равны 1, ф-ция в точке не определена.
Правильно ли я "нарешал"?
). Устранимый разрыв? Левый и правый пределы равны 1, ф-ция в точке не определена.
Правильно ли я "нарешал"?
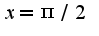 что касается точки
что касается точки 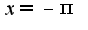 , то предел слева равен
, то предел слева равен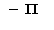 , а предел справа
, а предел справа 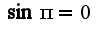 разрыв первого рода, функция непрерывна слева
разрыв первого рода, функция непрерывна слева