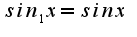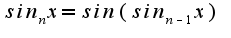Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Анатолий
#
8 ноя 2007 |
|
|
Максимович Игорь
#
8 ноя 2007 |
|
|
Анатолий
#
8 ноя 2007 |
|
|
Максимович Игорь
#
8 ноя 2007 |
|
|
Анатолий
#
8 ноя 2007 |
|
|
Максимович Игорь
#
8 ноя 2007 |
|
|
Максимович Игорь
#
8 ноя 2007 |
|
|
Анатолий
#
9 ноя 2007 |
|
|
Анатолий
#
9 ноя 2007 |
|
|
Анатолий
#
9 ноя 2007 |
|
|
Максимович Игорь
#
9 ноя 2007 |
|
|
Анатолий
#
9 ноя 2007 |
|
|
Анатолий
#
9 ноя 2007 |
|
|
Максимович Игорь
#
9 ноя 2007 |
|
|
Максимович Игорь
#
9 ноя 2007 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
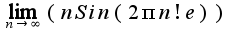
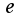 - основание натуральных логарифмов.
Пишите РЕШЕНИЯ, а не ответы.
Удачи! ;)
- основание натуральных логарифмов.
Пишите РЕШЕНИЯ, а не ответы.
Удачи! ;)
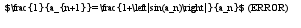 Легко показать, что
Легко показать, что 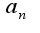 стремится к нулю при
стремится к нулю при 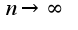 , оставаясь положительной величиной, а поэтому модуль у синуса можно убрать и разложить этот синус в ряд в окрестности нуля.
, оставаясь положительной величиной, а поэтому модуль у синуса можно убрать и разложить этот синус в ряд в окрестности нуля.
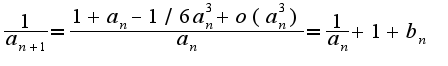
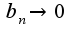 , когда
, когда 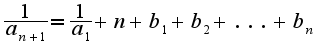
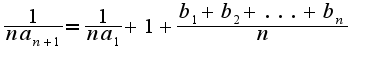 Переходя к пределу при
Переходя к пределу при 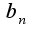 -ов равен
-ов равен 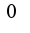 ):
):
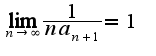 , что и есть ответом на изначальный вопрос.
, что и есть ответом на изначальный вопрос.
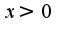 ):
): 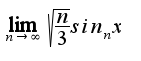 , где:
, где: