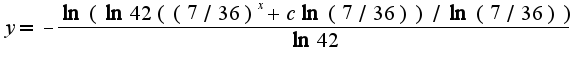Поиск
| Автор | Сообщение |
|---|---|
|
Лиза
#
21 июн 2008 |
|
|
О.А.
#
22 июн 2008 |
|
|
Лиза
#
22 июн 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
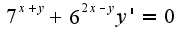 пробовала записать как
пробовала записать как 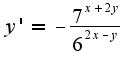 а дальше можно сделать так?
а дальше можно сделать так?
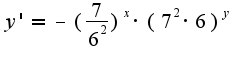 если можно, то как дальше?
если можно, то как дальше?
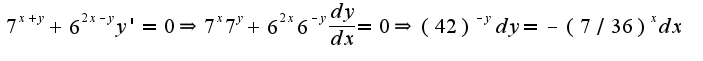 затем проинтегрировать
затем проинтегрировать