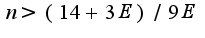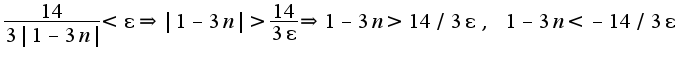Поиск
| Автор | Сообщение |
|---|---|
|
Юлия
#
31 янв 2009 |
|
|
О.А.
#
31 янв 2009 |
|
|
Юлия
#
1 фев 2009 |
|
|
lolechka
#
3 фев 2009 |
|
|
О.А.
#
3 фев 2009 |
|
|
lolechka
#
3 фев 2009 |
|
|
О.А.
#
3 фев 2009 |
|
|
lolechka
#
4 фев 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
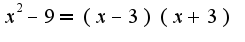 и сократите с числителем
и сократите с числителем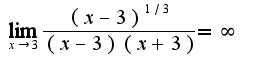
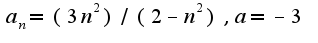 док-во
док-во
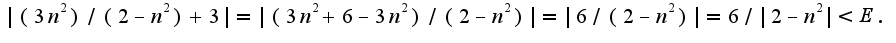
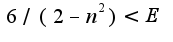
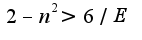
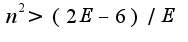
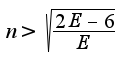 Из последнего неравенства следует, что можно выбрать
Из последнего неравенства следует, что можно выбрать ![$N(E)=[(2E-6)/E] $ $N(E)=[(2E-6)/E] $](http://teacode.com/service/latex/latex.png?latex=N%28E%29%3D%5B%282E-6%29%2FE%5D+&fontsize=21) вроде со знаками < > что-то не так... посмотрите пожалуйста
не пойму как делать когда степень у
вроде со знаками < > что-то не так... посмотрите пожалуйста
не пойму как делать когда степень у 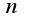 не 1, и когда в знаменателе так как тут например
не 1, и когда в знаменателе так как тут например
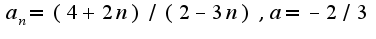 там получается
там получается
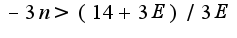 как тут найти
как тут найти 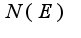 в книжке ничего не понятно, объясните пожалуйста.
в книжке ничего не понятно, объясните пожалуйста.
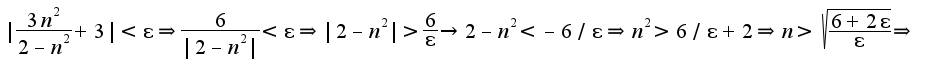
![$ N(\epsilon)=[\sqrt{\frac{6+2\epsilon}{\epsilon}}]$ $ N(\epsilon)=[\sqrt{\frac{6+2\epsilon}{\epsilon}}]$](http://teacode.com/service/latex/latex.png?latex=+N%28%5Cepsilon%29%3D%5B%5Csqrt%7B%5Cfrac%7B6%2B2%5Cepsilon%7D%7B%5Cepsilon%7D%7D%5D&fontsize=21) ,аналогично, и во втором примере нужно учесть,что в определении участвует модуль
,аналогично, и во втором примере нужно учесть,что в определении участвует модуль
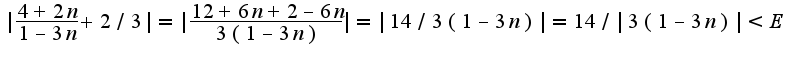 а здесь модуль раскрыть так
а здесь модуль раскрыть так
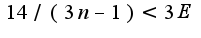 ->
-> 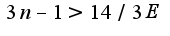 ->
-> 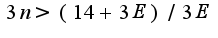 ->
->