Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
Прохор
#
17 ноя 2005 |
|
|
О.А.
#
17 ноя 2005 |
|
|
Прохор
#
17 ноя 2005 |
|
|
Прохор
#
18 ноя 2005 |
|
|
О.А.
#
18 ноя 2005 |
|
|
Станислав Матвеев
#
18 ноя 2005 |
|
|
Инкогнито
#
18 ноя 2005 |
|
|
О.А.
#
18 ноя 2005 |
|
|
О.А.
#
18 ноя 2005 |
|
|
???
#
20 ноя 2005 |
|
|
О.А.
#
20 ноя 2005 |
|
|
???
#
20 ноя 2005 |
|
|
Т.
#
25 ноя 2005 |
|
|
???
#
25 ноя 2005 |
|
|
О.А.
#
25 ноя 2005 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
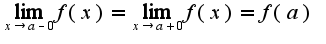 Что касается данной функции, то она непрерывна везде, за исключением точки
Что касается данной функции, то она непрерывна везде, за исключением точки 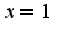 , т.е в точке, где знаменатель у степени 2 обращается в ноль. Поэтому ииследовать надо именно точку
, т.е в точке, где знаменатель у степени 2 обращается в ноль. Поэтому ииследовать надо именно точку 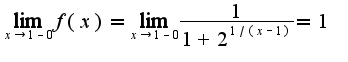 ,т.к.
,т.к. 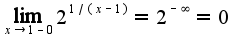 Рассуждая аналогично, получим, что
Рассуждая аналогично, получим, что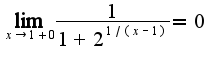 , т.к.
, т.к. 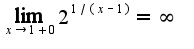
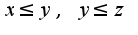 , то
, то 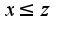 .
Вообще, если выполнены условия для отношения
.
Вообще, если выполнены условия для отношения 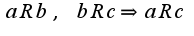 -транзитивность,
-транзитивность,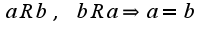 -антисимметричность, то данное отношение называется отношением порядка.Простым примером отношения порядка является отношение, задаваемое обычным неравенством на множестве вещественных чисел . Для любых чисел x и y выполняется либо
-антисимметричность, то данное отношение называется отношением порядка.Простым примером отношения порядка является отношение, задаваемое обычным неравенством на множестве вещественных чисел . Для любых чисел x и y выполняется либо 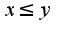 , либо
, либо 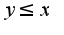 , т.е. любые два числа сравнимы между собой. Такие отношения называются отношениями полного порядка. Функционал-это числовая функция, определенная на некотором линейном пространстве.(см. учебник Колмогорова А.Н., Фомина С.В.)
, т.е. любые два числа сравнимы между собой. Такие отношения называются отношениями полного порядка. Функционал-это числовая функция, определенная на некотором линейном пространстве.(см. учебник Колмогорова А.Н., Фомина С.В.)
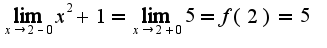
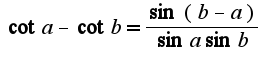 Затем использовать отрицание определения
Затем использовать отрицание определения 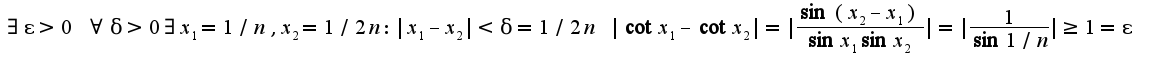 Данная функция не является равномерно непрерывной.
Данная функция не является равномерно непрерывной.
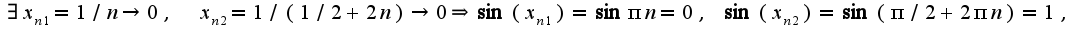 то есть получаем, что выполняется отрицание определения предела, т.к. значения на этих последовательностях разное, поэтому предела нет.
то есть получаем, что выполняется отрицание определения предела, т.к. значения на этих последовательностях разное, поэтому предела нет.