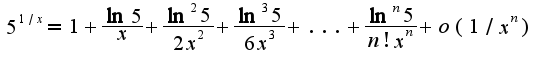Поиск
| Автор | Сообщение |
|---|---|
|
Дмитрий
#
23 янв 2008 |
|
|
Дмитрий
#
23 янв 2008 |
|
|
О.А.
#
23 янв 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
 с остаточным членом
с остаточным членом
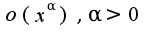
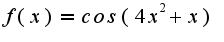
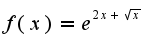 Найти асимптоты разложения функции при
Найти асимптоты разложения функции при 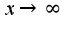 с остаточным членом
с остаточным членом 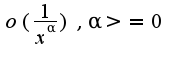
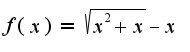
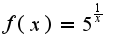 Пожалуйста помогите. Очень нужно. Большое спасибо.
Пожалуйста помогите. Очень нужно. Большое спасибо.
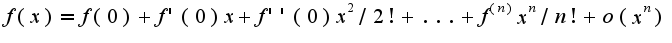 , применяя ее для функции
, применяя ее для функции 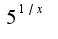 в точке
в точке 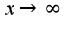 ,получим
,получим