Поиск
| Автор | Сообщение |
|---|---|
|
Pantera
#
17 апр 2006 |
|
|
О.А.
#
18 апр 2006 |
|
|
Pantera
#
18 апр 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
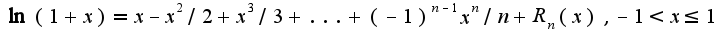 При
При 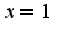 получим, что
получим, что 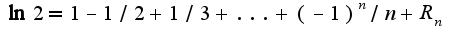 Из теории рядов известно, что данный ряд условно сходится.Он является рядом Лейбница, т.к. члены ряда образуют убываюшую последовательность и монотонно стремятся к нулю.Сл-но, число
Из теории рядов известно, что данный ряд условно сходится.Он является рядом Лейбница, т.к. члены ряда образуют убываюшую последовательность и монотонно стремятся к нулю.Сл-но, число 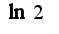 является иррациональным.
является иррациональным.