Поиск
| Автор | Сообщение |
|---|---|
|
Аня
#
27 мая 2007 |
|
|
О.А.
#
27 мая 2007 |
|
|
Аня
#
28 мая 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
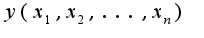 по одной ,например,
по одной ,например,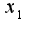 надо предположить, что остальные являются фиксированными числами.Например,
надо предположить, что остальные являются фиксированными числами.Например,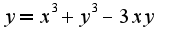 Находим производную по
Находим производную по  ,считаем
,считаем 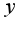 фиксированным числом,поэтому
фиксированным числом,поэтому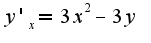 , аналогично,
, аналогично,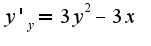 Тема "дифференциальное исчисление функции многих переменных" рассматривается в любом учебнике по математическому анализу, только книгу надо открыть.
Тема "дифференциальное исчисление функции многих переменных" рассматривается в любом учебнике по математическому анализу, только книгу надо открыть.