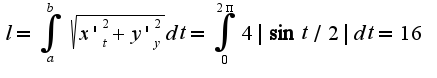Поиск
| Автор | Сообщение |
|---|---|
|
irada
#
2 мар 2009 |
|
|
О.А.
#
2 мар 2009 |
|
|
irada
#
2 мар 2009 |
|
|
О.А.
#
2 мар 2009 |
|
|
Александр
#
3 мар 2009 |
|
|
О.А.
#
3 мар 2009 |
|
|
Александр
#
3 мар 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
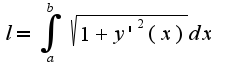 , т.к. функция
, т.к. функция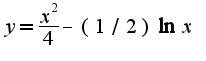 , то находим производную
, то находим производную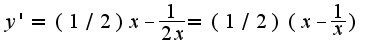 отсюда
отсюда 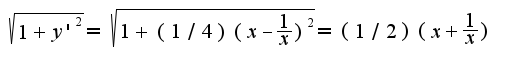 подставляя в формулу для длины, получим
подставляя в формулу для длины, получим