Поиск
| Автор | Сообщение |
|---|---|
|
Nastasya
#
24 окт 2013 |
|
|
o.a.
#
24 окт 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
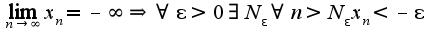 Для данного примера:
Для данного примера:
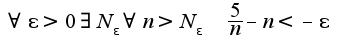 Решая данное неравенство, имеем
Решая данное неравенство, имеем 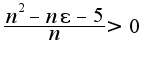 Так как
Так как 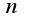 - натуральное число, то нужно лишь решить неравенство
- натуральное число, то нужно лишь решить неравенство 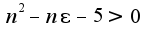 Решая, получим
Решая, получим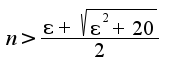 Сл-но, в качестве номера
Сл-но, в качестве номера ![$N_{\epsilon}=[\frac{\epsilon+\sqrt{\epsilon^2+20}}{2}]$ $N_{\epsilon}=[\frac{\epsilon+\sqrt{\epsilon^2+20}}{2}]$](http://teacode.com/service/latex/latex.png?latex=N_%7B%5Cepsilon%7D%3D%5B%5Cfrac%7B%5Cepsilon%2B%5Csqrt%7B%5Cepsilon%5E2%2B20%7D%7D%7B2%7D%5D&fontsize=21)