Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
69
#
10 мар 2006 |
|
|
О.А.
#
10 мар 2006 |
|
|
Лагранженко
#
10 мар 2006 |
|
|
О.А.
#
11 мар 2006 |
|
|
69
#
12 мар 2006 |
|
|
errant
#
12 мар 2006 |
|
|
О.А.
#
12 мар 2006 |
|
|
Chelovek
#
17 мар 2006 |
|
|
О.А.
#
17 мар 2006 |
|
|
Любопытный человек
#
25 мар 2006 |
|
|
О.А.
#
25 мар 2006 |
|
|
errant
#
26 мар 2006 |
|
|
О.А.
#
26 мар 2006 |
|
|
Chelovek
#
27 мар 2006 |
|
|
О.А.
#
27 мар 2006 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
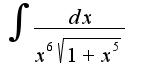
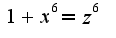 , а затем разложить на простейшие дроби
, а затем разложить на простейшие дроби
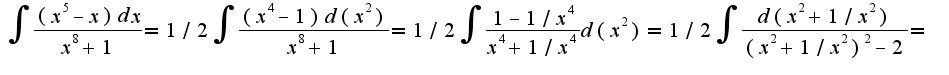
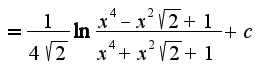 2)
2)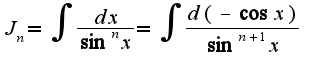 интегрируется по частям:
интегрируется по частям: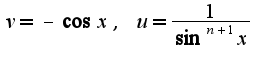 в результате получается рекуррентная формула:
в результате получается рекуррентная формула: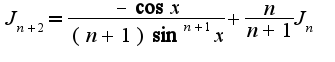
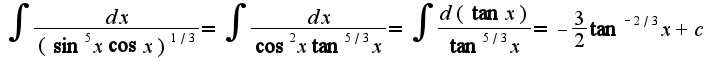
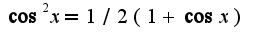
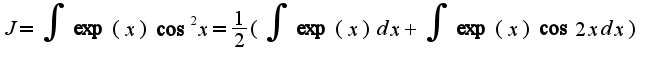 Второй интеграл берется по частям дважды.Получаем
Второй интеграл берется по частям дважды.Получаем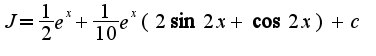
![$\int_{0}^{Pi/2}f(sinx)dx=\int_{0}^{Pi/2}f(cosx)dx, f-C_{[0,1]}$ $\int_{0}^{Pi/2}f(sinx)dx=\int_{0}^{Pi/2}f(cosx)dx, f-C_{[0,1]}$](http://teacode.com/service/latex/latex.png?latex=%5Cint_%7B0%7D%5E%7BPi%2F2%7Df%28sinx%29dx%3D%5Cint_%7B0%7D%5E%7BPi%2F2%7Df%28cosx%29dx%2C+f-C_%7B%5B0%2C1%5D%7D&fontsize=21)
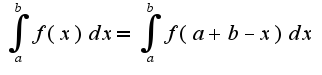 Поэтому
Поэтому 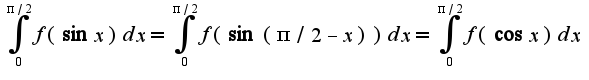
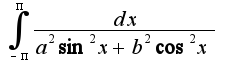 после интегрирования получается
после интегрирования получается 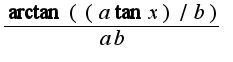 .
При дальнейшем вычислении определённого интеграла его значение становится равным 0, что не возможно.
Как решить эту проблему?
.
При дальнейшем вычислении определённого интеграла его значение становится равным 0, что не возможно.
Как решить эту проблему?
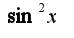 , тогда первообразная будет зависеть от
, тогда первообразная будет зависеть от 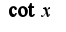 или первоначально разбить интеграл на сумму двух.
или первоначально разбить интеграл на сумму двух.