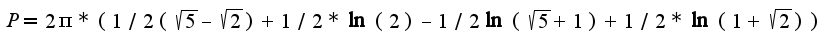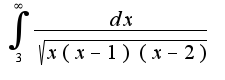Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
Chelovek
#
31 мар 2006 |
|
|
errant
#
31 мар 2006 |
|
|
О.А.
#
1 апр 2006 |
|
|
errant
#
1 апр 2006 |
|
|
Саврай Дарья
#
1 апр 2006 |
|
|
О.А.
#
1 апр 2006 |
|
|
Саврай Дарья
#
2 апр 2006 |
|
|
Yamish
#
7 апр 2006 |
|
|
Chelovek
#
7 апр 2006 |
|
|
О.А.
#
7 апр 2006 |
|
|
Chelovek
#
9 апр 2006 |
|
|
errant
#
9 апр 2006 |
|
|
О.А.
#
10 апр 2006 |
|
|
Chelovek
#
16 апр 2006 |
|
|
Chelovek
#
16 апр 2006 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
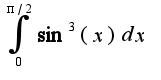 и
и 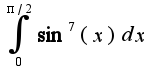
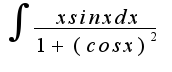
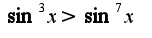 при
при 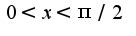 , то и
, то и 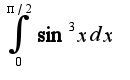 больше, чем
больше, чем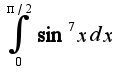 2) для ответа нужно указать пределы интегрирования
2) для ответа нужно указать пределы интегрирования
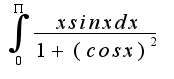
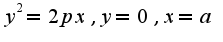 Найти -
Найти - 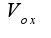 ?
?
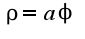 , найти
, найти 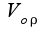
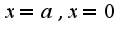 . Поэтому используем формулу для вычисления объма:
. Поэтому используем формулу для вычисления объма: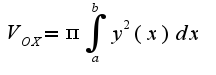
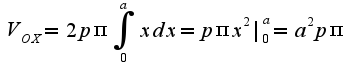 2)В этой задаче надо перейти в декартову систему координат по формулам:
2)В этой задаче надо перейти в декартову систему координат по формулам: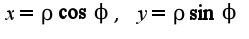 Формула для нахождения объема сохраняется:
Формула для нахождения объема сохраняется: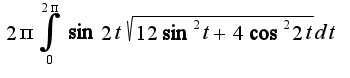
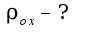
![$x-[0,\pi/{4}]$ $x-[0,\pi/{4}]$](http://teacode.com/service/latex/latex.png?latex=x-%5B0%2C%5Cpi%2F%7B4%7D%5D&fontsize=21)
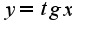 Затруднение вызывает взятие интеграла:
Затруднение вызывает взятие интеграла: 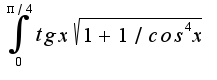 ?
?
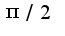 , затем полученную площадь умножить на два в силу симметрии фигуры, рекомендую построить в maple). Чтобы вычислить интеграл, надо преобразовать тригонометрическое выражение под корнем, затем сделать замену
, затем полученную площадь умножить на два в силу симметрии фигуры, рекомендую построить в maple). Чтобы вычислить интеграл, надо преобразовать тригонометрическое выражение под корнем, затем сделать замену 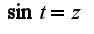 2)Сначала делать замену
2)Сначала делать замену 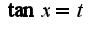 потом
потом 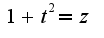 и наконец проинтегрировать полученный дифференциальный бином.У меня получился следующий ответ
и наконец проинтегрировать полученный дифференциальный бином.У меня получился следующий ответ