Поиск
| Автор | Сообщение |
|---|---|
|
Денис
#
11 июн 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
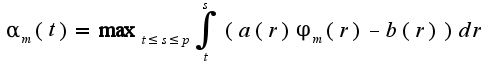 к функции
к функции 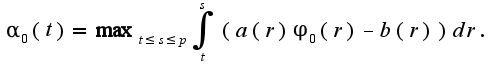
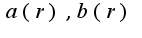 - непрерывные и неотрицательные на
- непрерывные и неотрицательные на ![$[t_0,p]$ $[t_0,p]$](http://teacode.com/service/latex/latex.png?latex=%5Bt_0%2Cp%5D&fontsize=21) ,
, 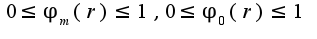 - измеримы на
- измеримы на ![$[t_0,p].$ $[t_0,p].$](http://teacode.com/service/latex/latex.png?latex=%5Bt_0%2Cp%5D.&fontsize=21) Доказал, что существует измеримая
Доказал, что существует измеримая 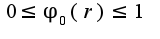 такая, что
такая, что 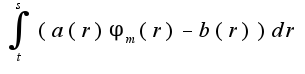 сходится к интегралу
сходится к интегралу 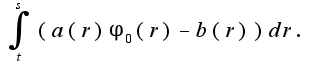 Как перейти теперь к максимуму? Может есть какие леммы/теоремы в помощь?
Как перейти теперь к максимуму? Может есть какие леммы/теоремы в помощь?