Поиск
| Автор | Сообщение |
|---|---|
|
Анастасия
#
18 янв 2009 |
|
|
О.А.
#
19 янв 2009 |
|
|
Анастасия
#
19 янв 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
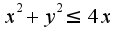 ;
; 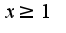 тут я сделала так:
тут я сделала так:
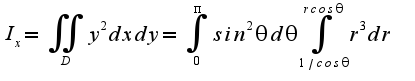 2. C помощью тройного интеграла вычислить объём тела, заданного неравенствами:
2. C помощью тройного интеграла вычислить объём тела, заданного неравенствами: 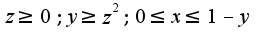
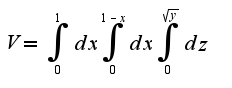 заранее спасибо
заранее спасибо
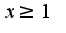 , поэтому
, поэтому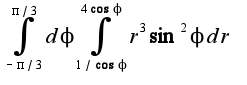 2)правильно
2)правильно