Dmitry
#
19 ноя 2009
|
Дано множество А= (0,1) U {-4} U (1,2). Надо было найти супремум и инфимум.
Я считаю, что sup(A)= 2; inf(A)=-4.
Надо доказать, что число 2 является наименьшей из верхних граней. Для доказательства я использовал свойства супремума.
1. Для любого x, принадл. множеству X, x<=sup{x}
2. Для любого EPS (эпсилон)>0 существует x > sup{x}-EPS
Т.е., если взять очень малое EPS, например, 0,000001, то при вычитании его из числа 2 обязательно найдется такое число x, которое уже не будет принадлежать данному множеству. Значит, число 2 является супремумом и наименьшей из верхних граней.
В чем неправильно данное доказательство? Мне сказали, что надо доказывать по-другому, и второе свойство супремума тут не при чем. Подскажите, пожалуйста, какое в данном случае должно быть доказательство?
|
О.А.
#
19 ноя 2009
|
по-моему мнению достаточно использовать определение точной верхней грани, а именно, 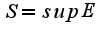 :
1) 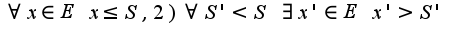 именно второе условие и гарантирует, что 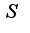 -минимальная среди верхних границ
у вас верно написано второе условие определения, но неправильно интерпретировано
|
Dmitry
#
20 ноя 2009
|
Большое спасибо, Ольга Александровна.
|
Dmitry
#
25 ноя 2009
|
Ольга Александровна, помогите, пожалуйста, еще раз с супремумом.
Дано множество А= (0,1) U {-4} U (1,2). Надо было найти супремум и инфимум.
supA=2.
Надо доказать, что число 2 является наименьшей из верхних граней.
Просто свойств супремума недостаточно.Доказательство требуется подробное. Следующие рассуждения признаны преподавателем правильными:
Докажем, что 2- наименьшая из верхних граней. Предположим противное, а именно: число 2 не является sup A и наименьшая верхняя грань меньше 2.
Пусть с=sup A, с<2, т.е.
для любого EPS (эпсилон)>0 с=2-EPS . Тогда найдется х, принадл. множеству А такое, что 2- EPS<x<2.
Остался такой вопрос: написать, чему в этом случае равен х (уравнение функции)
х=……
Помогите, пожалуйста. Мне казалось, что достаточно выражения 2-EPS<x<2. А какое уравнение функции надо написать, не могу сообразить.
Заранее благодарю.
|
О.А.
#
25 ноя 2009
|
кроме того, что я уже написала, мне нечего добавить, возможно ваша проблема в том, что вы недостаточно хорошо понимаете определение, поэтому и не можете пояснить свое доказательство, именно второе условие определения супремума и гарантирует, что это минимальная верхняя грань, так как найдется элемент множества, что 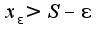 , таким образом, S-точная верхняя грань, а число 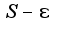 -не является точной верхней гранью
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
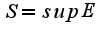 :
1)
:
1)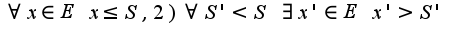 именно второе условие и гарантирует, что
именно второе условие и гарантирует, что 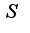 -минимальная среди верхних границ
у вас верно написано второе условие определения, но неправильно интерпретировано
-минимальная среди верхних границ
у вас верно написано второе условие определения, но неправильно интерпретировано
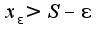 , таким образом, S-точная верхняя грань, а число
, таким образом, S-точная верхняя грань, а число 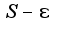 -не является точной верхней гранью
-не является точной верхней гранью