Поиск
| Автор | Сообщение |
|---|---|
|
Kolobok
#
11 апр 2009 |
|
|
Kolobok
#
11 апр 2009 |
|
|
Kolobok
#
12 апр 2009 |
|
|
О.А.
#
12 апр 2009 |
|
|
Kolobok
#
12 апр 2009 |
|
|
Kolobok
#
12 апр 2009 |
|
|
Kolobok
#
14 апр 2009 |
|
|
О.А.
#
14 апр 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
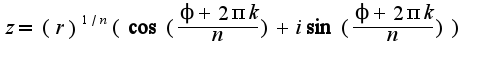 , где
, где 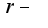 модуль комплексного числа,
модуль комплексного числа, 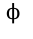 - аргумент
- аргумент
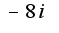 в тригонометрической форме
в тригонометрической форме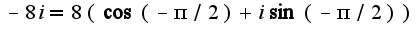 2)воспользоваться написанной выше формулой для
2)воспользоваться написанной выше формулой для