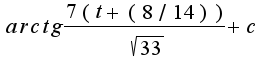Поиск
| Автор | Сообщение |
|---|---|
|
Олег
#
23 мар 2007 |
|
|
О.А.
#
23 мар 2007 |
|
|
Олег
#
23 мар 2007 |
|
|
О.А.
#
23 мар 2007 |
|
|
Олег
#
23 мар 2007 |
|
|
О.А.
#
23 мар 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
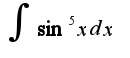
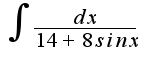
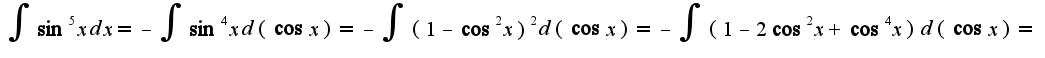
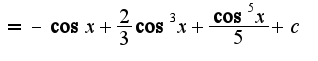 2)можно использовать универсальную тригонометрическую подстановку
2)можно использовать универсальную тригонометрическую подстановку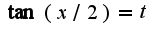
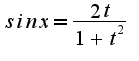
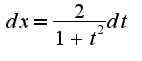 и в конце получил
и в конце получил 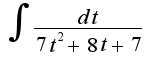 А дальше что делать?
А дальше что делать?
 *
*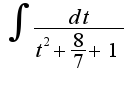 =
=
=
=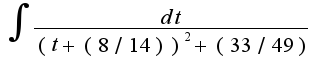 =
=
=
=