Поиск
| Автор | Сообщение |
|---|---|
|
Оля
#
7 дек 0714 |
|
|
О.А.
#
21 дек 2006 |
|
|
Оля
#
21 дек 2006 |
|
|
О.А.
#
21 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться

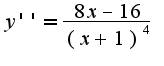 То есть
То есть 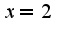 -точка перегиба, т.к. вторая производная меняет знак при переходе через эту точку. Если
-точка перегиба, т.к. вторая производная меняет знак при переходе через эту точку. Если 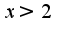 ,то функция выпукла вниз(
,то функция выпукла вниз(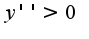 )если
)если 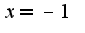 не входит в область определения.
не входит в область определения.
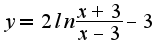 чётной или нечётной?
чётной или нечётной?
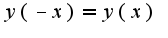 и нечетной функции(
и нечетной функции(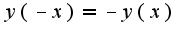 ).
).