Поиск
Александр
#
26 июн 2008
|
Доброго времени суток.
прошу помощи в решении моей задачи, проблема составить интегралы, вычислить я смогу.
дано, что область S ограничена линиями: y=x^(2)/2, y=x^(2)/3, y=x
нужно вычислить площадь этой области, объём, получающийся при вращении вокруг оси Х и выразить периметр (не вычисляя его) через определённые интегралы
что касается площади, то я построил эту область, там вроде получится
инт (от 0 до 2) (х - х^2/2)dx + инт (от 2 до 3) (х - х^2/3)dx
ПРАВИЛЬНО?
а вот объём и периметр незнаю, помогите, пожалуйста.
большое спасибо
|
О.А.
#
26 июн 2008
|
мне кажется, что область заключена между параболами, и прямой и параболой, советую уточнить у своего преподавателя,т.е. площадь находится по формуле: 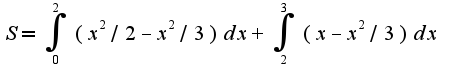 Формула для нахождения объема тела вращения 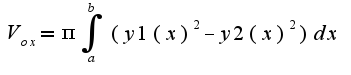
|
Александр
#
26 июн 2008
|
Извините меня, но можно я спрошу у вас:
V = пи * интеграл(от 0 до 3) от [(x^2/2)^2-(x^2/3)^2]dx
ТАК?
а насчёт выражения периметра не подскажите?
|
О.А.
#
26 июн 2008
|
для нахождения объма также нужно разбить на две подобласти, что касается периметра, то длина дуги находится по формуле 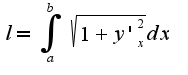 , данная область образована тремя линиями, длину каждой надо найти по указанной формуле, учитывая координаты
|
Александр
#
27 июн 2008
|
извините за навязчивость, просто это одно задание одно осталось, нужно доразбираться.
посмотрите, я правильно понял:
V= пи * инт(от 0 до 2) ((x^2/2)^2-(x^2/3)^2)dx + пи * инт(от 2 до 3) [(x)^2-(x^2/3)^2]dx
и
l= инт(от 0 до 2) корень из 1+[производная(x^2/2)]^2dx + инт(от 2 до 3) корень из 1+[производная(x)]^2 dx + инт(от 0 до 3) корень из 1+[производная(x^2/3)]^2dx
ТАК?
очень надеюсь на вашу помощь
p.s. к сожалению не умею писать формулами как вы, ещё не научился.
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
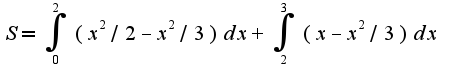 Формула для нахождения объема тела вращения
Формула для нахождения объема тела вращения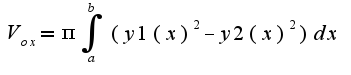
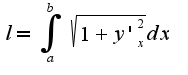 , данная область образована тремя линиями, длину каждой надо найти по указанной формуле, учитывая координаты
, данная область образована тремя линиями, длину каждой надо найти по указанной формуле, учитывая координаты