Поиск
| Автор | Сообщение |
|---|---|
|
Андрей М.
#
21 янв 2009 |
|
|
О.А.
#
22 янв 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
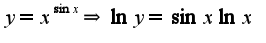 , сл-но,
, сл-но,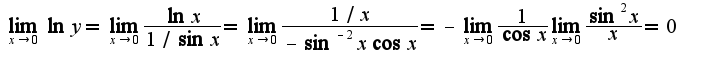 , отсюда следует, что
, отсюда следует, что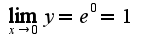 при решении использован первый замечательный предел
при решении использован первый замечательный предел