Поиск
| Автор | Сообщение |
|---|---|
|
незнайка
#
17 дек 2006 |
|
|
О.А.
#
18 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
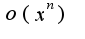 , то запись
, то запись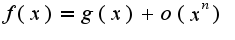 означает, что функция
означает, что функция 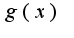 -является главной частью функции
-является главной частью функции 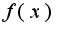 остальные слагаемые являются бесконечно малыми более высокого порядка малости по сравнению с
остальные слагаемые являются бесконечно малыми более высокого порядка малости по сравнению с 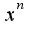 .Если это символ
.Если это символ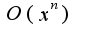 , то это означает, что остальные слагаемые ограничены по сравнению с функцией
, то это означает, что остальные слагаемые ограничены по сравнению с функцией 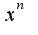 в окрестности
в окрестности 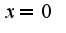 ,известно, что если
,известно, что если 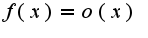 , то тем более
, то тем более 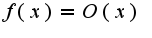 по некоторой базе.
по некоторой базе.