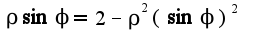Поиск
| Автор | Сообщение |
|---|---|
|
1988
#
6 ноя 2006 |
|
|
О.А.
#
6 ноя 2006 |
|
|
1988
#
6 ноя 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
 В полярных:
В полярных: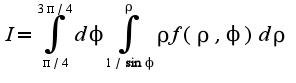 , где
, где 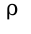 определяется из уравнения:
определяется из уравнения: