Поиск
| Автор | Сообщение |
|---|---|
|
Артём
#
15 дек 2006 |
|
|
Аотём
#
16 дек 2006 |
|
|
О.А.
#
16 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
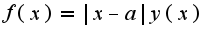 , где
, где 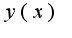 - непрерывная функция и
- непрерывная функция и 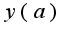 не равна
не равна 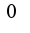 , не имеет производной в точке
, не имеет производной в точке 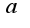 . Чему равны односторонние производные
. Чему равны односторонние производные 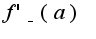 и
и 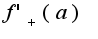 ?
Найти
?
Найти 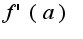 , если
, если 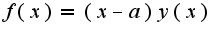 , где функция
, где функция 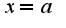 .
Заранее благодарен.
.
Заранее благодарен.
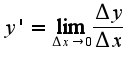 Находим
Находим 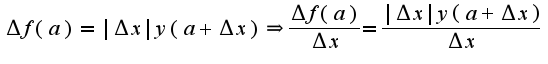 Сл-но, предела нет, но есть односторонние пределы:
Сл-но, предела нет, но есть односторонние пределы: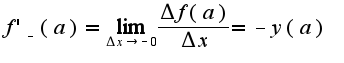 и
и 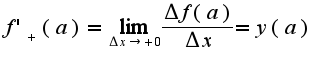 Отсюда следует, что
Отсюда следует, что 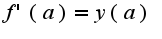 , если
, если