Поиск
Василий
#
29 янв 2007
|
Дано задание:
Исследовать функцию на непрерывность
y = (2x^2+5y-3)/(|x+3|(x+2))
найти точки разрыва, исследоать их характер. Найти вертикальные и горизонтальные асимптоты, и построить схематический график функции.
а) Точки разрыва я нашел
x0 = -3
x0 = -2
f(-3-0) = +00
f(-3+0) = -00 --> точка разрыва 2 рода
f(-2-0) = +00
f(-2+0) = -00 --> точка разрыва 2 рода
б) Асимптоты
Вертикальные х=-3 х=-2
а вот с горизонтальными какая-то неразбериха, даже построив график по точкам, я не понял какими должны быть горизонтальные асимптомы, хотя по графику видно, что слева график стремиться к у=-1, а справа к y=1.
Подскажите пожалуста, как даделать этот пример?
|
О.А.
#
29 янв 2007
|
Надо преобразовать функцию, расписать модуль, тогда станет ясно, что горизонтальные асимптоты: 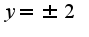 Кроме того, 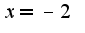 -разрыв второго рода, а точка 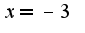 -первого рода,т.к. в ней существуют односторонние пределы, неравные по значению, вид графика
http://www.matan.isu.ru/kons16.gif
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
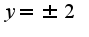 Кроме того,
Кроме того, 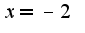 -разрыв второго рода, а точка
-разрыв второго рода, а точка 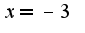 -первого рода,т.к. в ней существуют односторонние пределы, неравные по значению, вид графика
http://www.matan.isu.ru/kons16.gif
-первого рода,т.к. в ней существуют односторонние пределы, неравные по значению, вид графика
http://www.matan.isu.ru/kons16.gif