Поиск
| Автор | Сообщение |
|---|---|
|
Студент
#
15 янв 2006 |
|
|
О.А.
#
15 янв 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
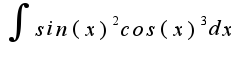 и как исследовать сходимость ряда
и как исследовать сходимость ряда
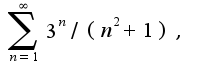
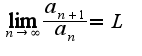 Если
Если 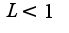 , то ряд сходится, если
, то ряд сходится, если 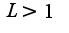 , то ряд расходится. Для данного ряда
, то ряд расходится. Для данного ряда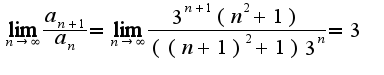 Сл-но, ряд расходится.
Что касается интеграла, наверное условие Вы неправильно написали,я думаю, что такой интеграл:
Сл-но, ряд расходится.
Что касается интеграла, наверное условие Вы неправильно написали,я думаю, что такой интеграл: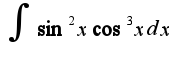 , чтобы его вычислить надо преобразовать подинтегральное выражение, а именно:
, чтобы его вычислить надо преобразовать подинтегральное выражение, а именно: