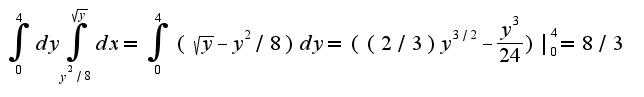Поиск
| Автор | Сообщение |
|---|---|
|
Светлана
#
15 янв 2007 |
|
|
О.А.
#
15 янв 2007 |
|
|
Светлана
#
15 янв 2007 |
|
|
О.А.
#
16 янв 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
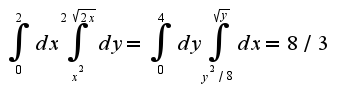
 , а затем по переменной
, а затем по переменной 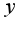 , ответ естественно совпадает и равен 8/3
, ответ естественно совпадает и равен 8/3