Поиск
| Автор | Сообщение |
|---|---|
|
nou3
#
9 мар 2007 |
|
|
О.А.
#
10 мар 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
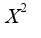
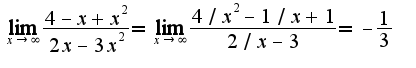 Если применять правило Лопиталя, то надо продифференцировать числитель и знаменатель,т.е.
Если применять правило Лопиталя, то надо продифференцировать числитель и знаменатель,т.е.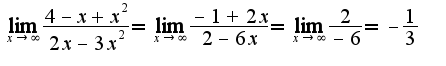 2)
2)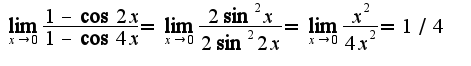 По правилу Лопиталя также нужно дифференцировать числитель и знаменатель, кроме того, надо учесть
По правилу Лопиталя также нужно дифференцировать числитель и знаменатель, кроме того, надо учесть 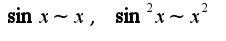 при
при