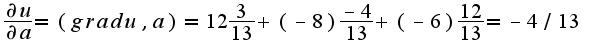Поиск
| Автор | Сообщение |
|---|---|
|
Екатерина
#
22 мая 2005 |
|
|
О.А.
#
22 мая 2005 |
|
|
Ольга Шабалина
#
27 мая 2005 |
|
|
О.А.
#
27 мая 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
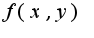 называется непрерывной в точке
называется непрерывной в точке 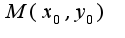 , если выполняется равенство
, если выполняется равенство 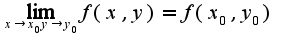
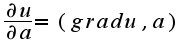 , где
, где 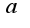 -единичный вектор,т.е.
-единичный вектор,т.е. 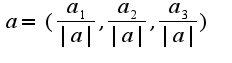 . Следовательно,
. Следовательно,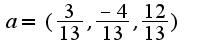 Поэтому,
Поэтому,