Поиск
| Автор | Сообщение |
|---|---|
|
Константин
#
27 мар 2008 |
|
|
О.А.
#
27 мар 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
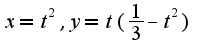 Пожалуйста помогите!!! Заранее спасибо!!!
Пожалуйста помогите!!! Заранее спасибо!!!
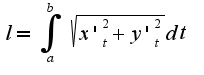 Нужно построить график данной кривой для того, чтобы найти пределы интегрирования
Нужно построить график данной кривой для того, чтобы найти пределы интегрирования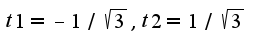 ,таким образом получим
,таким образом получим