Поиск
| Автор | Сообщение |
|---|---|
|
Ирина
#
15 дек 2006 |
|
|
О.А.
#
15 дек 2006 |
|
|
Ирина
#
15 дек 2006 |
|
|
О.А.
#
15 дек 2006 |
|
|
Ирина
#
15 дек 2006 |
|
|
Ирина
#
15 дек 2006 |
|
|
О.А.
#
15 дек 2006 |
|
|
Ирина
#
15 дек 2006 |
|
|
Ирина
#
15 дек 2006 |
|
|
О.А.
#
15 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
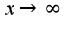 данная функция является бесконечно большой, поэтому
данная функция является бесконечно большой, поэтому 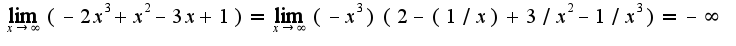 , т.к.
, т.к. 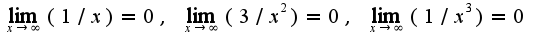
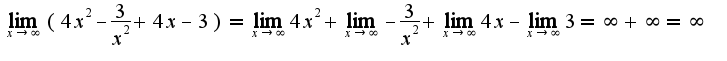
 , то есть на
, то есть на 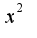 Смотрите тему нашей консультации http://www.teacode.com/forum/show-thread.jsp?forum=0&thread=2018&page=0&answers=5
Там решен подобный пример.
В дополнение к предыдущему примеру
Смотрите тему нашей консультации http://www.teacode.com/forum/show-thread.jsp?forum=0&thread=2018&page=0&answers=5
Там решен подобный пример.
В дополнение к предыдущему примеру