Поиск
| Автор | Сообщение |
|---|---|
|
ritaivan94
#
11 ноя 2013 |
|
|
o.a.
#
11 ноя 2013 |
|
|
ritaivan94
#
11 ноя 2013 |
|
|
o.a.
#
11 ноя 2013 |
|
|
ritaivan94
#
12 ноя 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
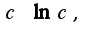 то есть решение имеет вид
то есть решение имеет вид 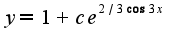 2)интеграл можно найти только применяя интегрирование по частям
2)интеграл можно найти только применяя интегрирование по частям
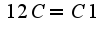 все равно константа
все равно константа