Поиск
Катя
#
26 мар 2009
|
Найти моменты инерции относительно осей координат плоской однородной фигуры, ограниченной кривыми: xy=4, xy=8, x=2y, 2x=y, x>=0, y>=0
Построила графики, получилась фигура:
корень(2)<=x<=4 4/корень(8)<=y<=4 (так изменяется x и y, т.е. область D ???)
Судя по формуле, нужно взять двойной интеграл:
I=int int (x^2+y^2)dxdy по области D.
У меня проблема, что не понимаю ЧТО нужно писать в подынтегральном выражении в моем задании, и сомнение по поводу правильности определения области D. Подскажите, пожалуйста! Заранее большое спасибо!
|
О.А.
#
26 мар 2009
|
моменты инерции однородной пластины относительно осей считаются по формулам 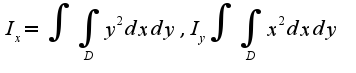 нужно ввести замену переменных,т.к. область сложная, и чтобы пределы расставить, надо ее подразделить на подобласти, поэтому проще сделать замену ![$xy=u,x/y=v,u\in[4,8],v\in[1/2,2]$ $xy=u,x/y=v,u\in[4,8],v\in[1/2,2]$](http://teacode.com/service/latex/latex.png?latex=xy%3Du%2Cx%2Fy%3Dv%2Cu%5Cin%5B4%2C8%5D%2Cv%5Cin%5B1%2F2%2C2%5D&fontsize=21)
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
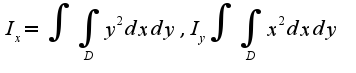 нужно ввести замену переменных,т.к. область сложная, и чтобы пределы расставить, надо ее подразделить на подобласти, поэтому проще сделать замену
нужно ввести замену переменных,т.к. область сложная, и чтобы пределы расставить, надо ее подразделить на подобласти, поэтому проще сделать замену![$xy=u,x/y=v,u\in[4,8],v\in[1/2,2]$ $xy=u,x/y=v,u\in[4,8],v\in[1/2,2]$](http://teacode.com/service/latex/latex.png?latex=xy%3Du%2Cx%2Fy%3Dv%2Cu%5Cin%5B4%2C8%5D%2Cv%5Cin%5B1%2F2%2C2%5D&fontsize=21)