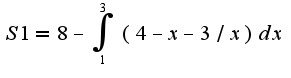Поиск
Tatyana_M
#
22 янв 2009
|
О.К. Проблема осталась.
Нужно: площадь фигуры, ограниченной линиями х+y-4=0 и xy=3 и осями координат.
Я запуталась вовсе: на данный момент у меня есть 2 варианта решения:
1. Пределы интегрирования - решением являются две точки: х1=1, у1=3 и х2=3, у2=1.
Соответственно выражение нахождения площади будет другое:
Площадь равна int(предел от 3 до 1)(4-x-3/x)dx=(4x-х^2/2-3ln[x]) от 3 до 1 = 4-3ln3 =0,704 (кВ.ед.)
То есть в данном случае пределы интегрирования совсем другие – как же правильно???
2. Второй вариант решения – другие пределы интегрирования: от 0 до1, от 1 до 3 и ль 3 до 4.
площадь равна int(пределы от 0 до 1)(4-x)dx+int(от 1 до 3)(3/x)dx+int(от 3 до 4)(4-x)dx=
правда ответ и тут все равно не получается.
Как быть я уже зашорилась и запуталась – помогите разобраться!!! Уже завтра надо сдавать исправленное – а я в потьмах.
|
О.А.
#
22 янв 2009
|
вот и уточните у своего преподавателя, что имелось в виду под фигурой, ограниченной осями координат, ясно, что фигура, ограничена сверху прямой 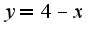 , снизу гиперболой 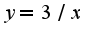 , если подключать в рассмотрение оси координат, то из площади треугольника надо вычесть площадь найденной фигуры,т.е. 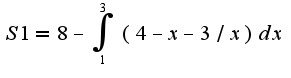
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
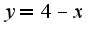 , снизу гиперболой
, снизу гиперболой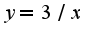 , если подключать в рассмотрение оси координат, то из площади треугольника надо вычесть площадь найденной фигуры,т.е.
, если подключать в рассмотрение оси координат, то из площади треугольника надо вычесть площадь найденной фигуры,т.е.