Поиск
| Автор | Сообщение |
|---|---|
|
asd
#
20 дек 2005 |
|
|
О.А.
#
20 дек 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
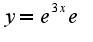 Тогда используя известное разложение по формуле Маклорена для функции
Тогда используя известное разложение по формуле Маклорена для функции 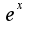 , получим:
, получим: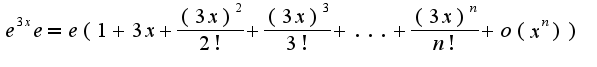 Здесь записан остаточный член в форме Пеано, поэтому данная формула носит название локальной, т.е. при
Здесь записан остаточный член в форме Пеано, поэтому данная формула носит название локальной, т.е. при 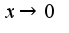 Если пренебречь остаточным членом, то получится ряд для
Если пренебречь остаточным членом, то получится ряд для 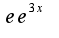 , который сходится
, который сходится 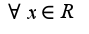 , т.к. радиус сходимости равен бесконечночти.(Радиус сходимости определяется по формуле
, т.к. радиус сходимости равен бесконечночти.(Радиус сходимости определяется по формуле 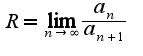 )Здесь
)Здесь