Поиск
| Автор | Сообщение |
|---|---|
|
Наташа
#
13 окт 2008 |
|
|
Наташа
#
14 окт 2008 |
|
|
О.А.
#
14 окт 2008 |
|
|
Наташа
#
15 окт 2008 |
|
|
О.А.
#
15 окт 2008 |
|
|
Наташа
#
15 окт 2008 |
|
|
Настя
#
15 окт 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
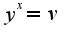 ,
,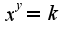 , затем прологарифмируйте
, затем прологарифмируйте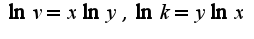 , затем находите производные
, затем находите производные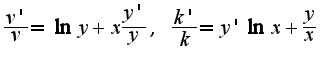
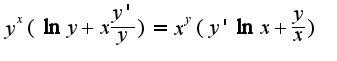 из данного уравнения надо найти
из данного уравнения надо найти 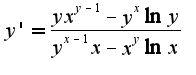
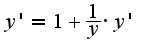 отсюда выражайте
отсюда выражайте 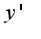 , это и будет ответ, вроде так
, это и будет ответ, вроде так