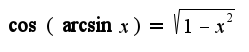Поиск
Федюн
#
26 дек 2007
|
Здравствуйте, Ольга Александровна!
Проверьте, пожалуйста задачу, а точнее - ее начало, а то дальше что-то не то получается.
Задача:
из металлической заготовки в форме круга радиуса R вырезают сектор с центр. углом 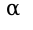 . Найти такое значение этого угла, при котором объем конуса, полученного свертыванием этого сектора, будет максимальным.
Вот, что я решил:
Пусть 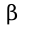 - 1/2 угла при вершине конуса; h - высота конуса; L=R - образующая конуса; 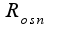 - радиус основания конуса.
Тогда площадь сектора будет равна бок. площади конуса.
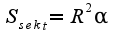 , 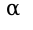 в радианной мере.
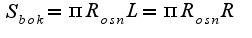 , где 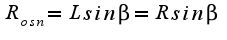 ,
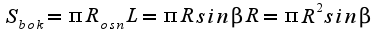 ,
Приравняем площади: 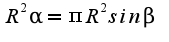
Получим: 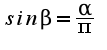 или 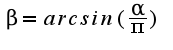
Объем конуса:
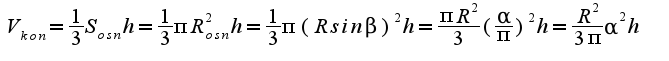
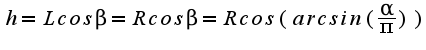
Тогда:
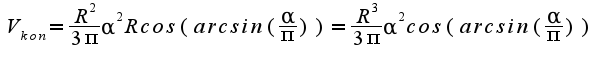
А дальше через первую производную решаем.
Только вот вопрос - правильно ли все сделано, а то производная получается сложной и найти ее нулевые значения непросто - там и синус, и косинус от арксинуса...
Заранее благодарю за помощь.
|
О.А.
#
26 дек 2007
|
Здравствуйте! По-моему, ход решения верный, только площадь сектора 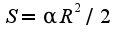 и еще известна формула 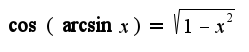
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
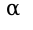 . Найти такое значение этого угла, при котором объем конуса, полученного свертыванием этого сектора, будет максимальным.
Вот, что я решил:
Пусть
. Найти такое значение этого угла, при котором объем конуса, полученного свертыванием этого сектора, будет максимальным.
Вот, что я решил:
Пусть 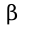 - 1/2 угла при вершине конуса; h - высота конуса; L=R - образующая конуса;
- 1/2 угла при вершине конуса; h - высота конуса; L=R - образующая конуса; 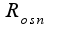 - радиус основания конуса.
Тогда площадь сектора будет равна бок. площади конуса.
- радиус основания конуса.
Тогда площадь сектора будет равна бок. площади конуса.
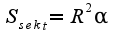 ,
, 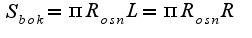 , где
, где 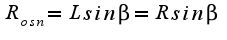 ,
,
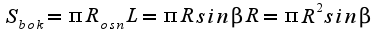 ,
Приравняем площади:
,
Приравняем площади: 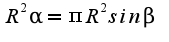 Получим:
Получим: 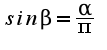 или
или 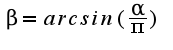 Объем конуса:
Объем конуса:
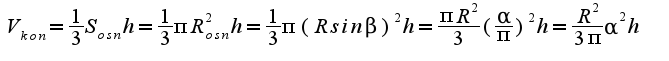
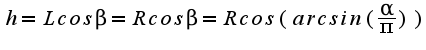 Тогда:
Тогда:
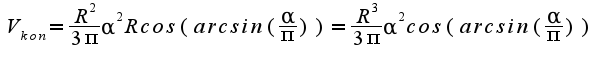 А дальше через первую производную решаем.
Только вот вопрос - правильно ли все сделано, а то производная получается сложной и найти ее нулевые значения непросто - там и синус, и косинус от арксинуса...
Заранее благодарю за помощь.
А дальше через первую производную решаем.
Только вот вопрос - правильно ли все сделано, а то производная получается сложной и найти ее нулевые значения непросто - там и синус, и косинус от арксинуса...
Заранее благодарю за помощь.
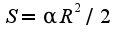 и еще известна формула
и еще известна формула