| Автор | Сообщение |
|---|---|
|
Станислав Матвеев
#
4 мая 2005 |
|
|
О.А.
#
4 мая 2005 |
|
|
О.А.
#
6 мая 2005 |
|
|
Станислав Матвеев
#
8 мая 2005 |
|
|
О.А.
#
8 мая 2005 |
|
|
Николай
#
10 июн 2005 |
|
|
О.А.
#
10 июн 2005 |
|
|
Юрий
#
10 июн 2005 |
|
|
О.А.
#
10 июн 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
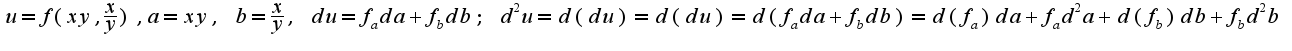 ,где
,где
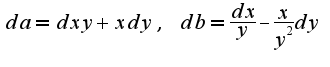 , кроме того,
, кроме того, 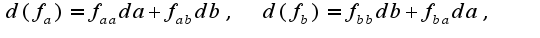 Причем,
Причем, 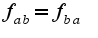 Также,
Также, 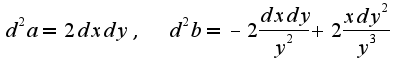 Остальное я уже писала в предыдущем ответе.
Остальное я уже писала в предыдущем ответе.
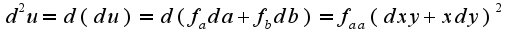
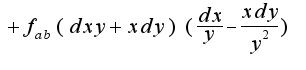
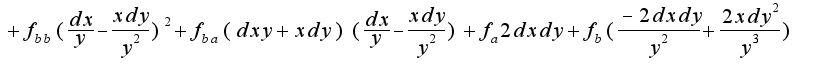
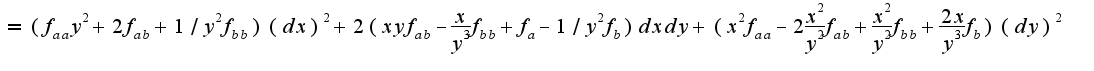
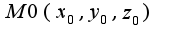 для функции, заданной неявно
для функции, заданной неявно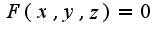 , имеет вид:
, имеет вид: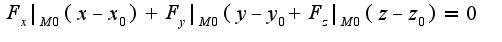 Поэтому находим частные производные от данной функции
Поэтому находим частные производные от данной функции 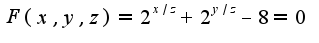 по x,y,z и считаем их в указанной точке
по x,y,z и считаем их в указанной точке 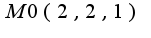 .
. 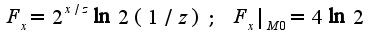
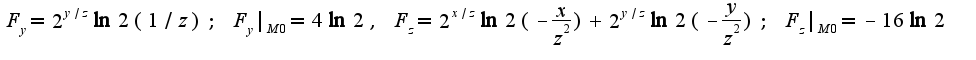 . Сл-но, уравнение касательной плоскости имеет вид:
. Сл-но, уравнение касательной плоскости имеет вид: 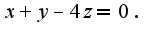
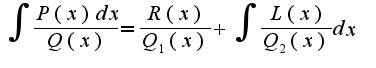 , где
, где 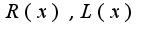 -многочлены с неопределенными коэффициентами, степени которых на единицу меньше степеней многочленов
-многочлены с неопределенными коэффициентами, степени которых на единицу меньше степеней многочленов 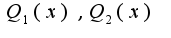 . Причем
. Причем 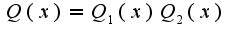 и у многочлена
и у многочлена 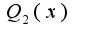 корни все простые и каждый его корень является корнем многочлена
корни все простые и каждый его корень является корнем многочлена 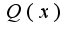 . Неопределенные коэффициенты находятся при помощи дифференцирования указанного выше равенства.
. Неопределенные коэффициенты находятся при помощи дифференцирования указанного выше равенства.