Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Поиск| Автор | Сообщение |
|---|---|
|
Cheetah
#
15 фев 2013 |
|
|
o_a
#
15 фев 2013 |
|
|
Cheetah
#
15 фев 2013 |
|
|
Pavel276
#
16 фев 2013 |
|
|
o_a
#
16 фев 2013 |
|
|
Елена
#
26 мар 2013 |
|
|
Елена
#
26 мар 2013 |
|
|
ustinova
#
25 апр 2013 |
|
|
o.a.
#
25 апр 2013 |
|
|
Маришка
#
3 июн 2013 |
|
|
o.a.
#
3 июн 2013 |
|
|
Тата
#
8 дек 2013 |
|
|
o_a
#
8 дек 2013 |
|
|
Тата
#
8 дек 2013 |
|
|
big_food
#
9 янв 2014 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
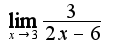
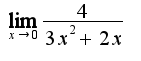
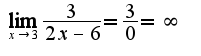
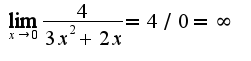
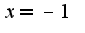 ,который можно найти, используя правило Лопиталя, то предел слева и справа в этой точке равны, рекомендую прочитать учебник по математическому анализу, раздел "предел функции".
,который можно найти, используя правило Лопиталя, то предел слева и справа в этой точке равны, рекомендую прочитать учебник по математическому анализу, раздел "предел функции".
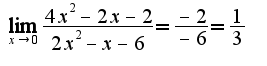 2)поскольку
2)поскольку 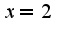 является корнем числителя и знаменателя, то нужно сократить дробь на общий множитель
является корнем числителя и знаменателя, то нужно сократить дробь на общий множитель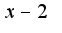 , затем подставить предельную точку, ответ
, затем подставить предельную точку, ответ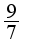 3)нужно поделить числитель и знаменатель на
3)нужно поделить числитель и знаменатель на 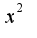 , учесть, что выражения
, учесть, что выражения 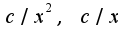 стремятся к нулю при
стремятся к нулю при 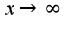 поэтому предел равен2
поэтому предел равен2
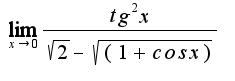 Домножаю числитель и знаменатель на
Домножаю числитель и знаменатель на 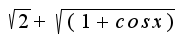 , получаю
, получаю
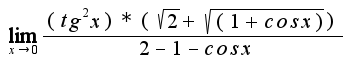 =
= 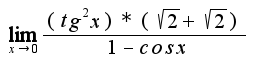 А дальше?
А дальше?
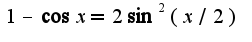 , а также замену эквивалентных:
, а также замену эквивалентных: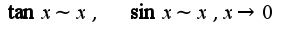 Сл-но,
Сл-но,