Поиск
| Автор | Сообщение |
|---|---|
|
Наталия
#
20 окт 2006 |
|
|
О.А.
#
20 окт 2006 |
|
|
Наталия
#
23 окт 2006 |
|
|
Наталия
#
23 окт 2006 |
|
|
О.А.
#
23 окт 2006 |
|
|
Наталия
#
24 окт 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
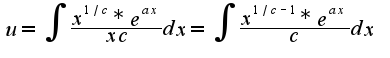 Т.к. число «с» из условий принимает достаточно большое значение (с=-1641), то 1/c стремится к 0, тогда можно заменить
Т.к. число «с» из условий принимает достаточно большое значение (с=-1641), то 1/c стремится к 0, тогда можно заменить
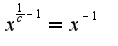 откуда получаем
откуда получаем
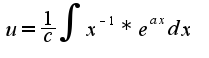 а дальше интеграл не берется :(
или надо было другим способом начинать решать?
вот если бы не было этого коэффициента "с" в уравнении, все было бы просто замечательно и просто, он все только спутал :(
а дальше интеграл не берется :(
или надо было другим способом начинать решать?
вот если бы не было этого коэффициента "с" в уравнении, все было бы просто замечательно и просто, он все только спутал :(
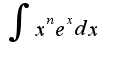 при условии, что n - целое положительное число, а в моем случае n=-1, т.е. оно отрицательное. как быть?
при условии, что n - целое положительное число, а в моем случае n=-1, т.е. оно отрицательное. как быть?