Teacode.com: К экзамену

Страницы: 1 2 3 4 5 6 7

Автор	Сообщение
О.А. # 6 июн 2005	Здравствуйте, Юра. Задача будет формулироваться следующим образом: исследовать на сходимость, признак Вы должны сами выбрать. Если будут трудности, какой признак применить, можно у меня спросить. Примеры на ряды достаточно простые.
Екатерина # 6 июн 2005	Добрый вечер, Ольга Александровна! Скажите, пожалуйста, нужно ли учить доказательства формулы Бонне или будет достаточно знать ее формулировку. Заранее благодарю.
О.А. # 7 июн 2005	Добрый вечер, Катя. Достаточно знать формулировку второй теоремы о среднем.
Юрий # 7 июн 2005	Здравствуйте, Ольга Александровна! Скажите, будут ли примеры, где надо будет исследовать неявную функцию на локальный экстремум!
Марченкова Анастасия # 7 июн 2005	Здравствуйте, Ольга Александровна. Нужно ли доказывать формулу Тейлора с остаточным членом в форме Пеано, Лагранжа и в интегральной форме или только с каким-нибудь одним?
О.А. # 8 июн 2005	Здравствуйте, Юра. Таких примеров не будет, нужно уметь находить дифференциалы первого и второго порядка от неявно заданной функции, а также знать уравнение касательной плоскости для неявно заданной функции.
О.А. # 8 июн 2005	Здравствуйте, Настя. Теорема Тейлора нужна без доказательства, но необходимо знать, как записывается остаточный член в форме Лагранжа, Пеано.
Ольга Шабалина # 8 июн 2005	Здравствуйте, Ольга Александровна. Скажите пожалуйста по какому учебнику нужно учить 41 билет, а то я никак не могу найти эту тему.
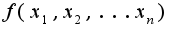О.А. # 8 июн 2005	Здравствуйте, Оля. Если речь идет о вопросе "Наибольшее и наименьшее значения непрерывных функций нескольких переменных", то этот вопрос носит больше практическое значение, т.к. завершает вопрос о существовании локального экстремума функции нескольких переменных. Пусть функция -дифференцируема на открытом и ограниченном множестве и непрерывна на его замыкании, тогда по теореме Вейерштрасса существует точная верхняя и нижняя грани зхначений функции на этом множестве. Для нахождения наибольшего и наименьшего значений надо найти все стационарные точки функции на указанном множестве, вычислить значения в них и выбрать точки, где функция принимает наибольшее и наименьшее значения из всех значений в стационарных точках. После этого надо найти значения на границе множества и сравнить значения на границе со значениями в стационарных точках, таким образом находятся наибольшее и наименьшее значения на множестве. Рекомендую решить пример 3. Найти наибольшее и наименьшее значения функции 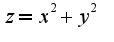на эллипсе
Станислав Матвеев # 9 июн 2005	Здравствуйте Ольга Александровна,нужно ли в геометрических приложениях определённого интеграла рассказывать про понятия простой, параметризуемой, спремляемой кривой?
О.А. # 9 июн 2005	Здравствуйте, Станислав. При изложении вопроса про длину дуги плоской кривой надо ограничиться определением длины дуги и выводом формулы для вычисления длины дуги в декартовых, полярных координатах и если кривая задана параметром. Ориентироваться надо на учебник М.С.Красса " Математика для экономических специальностей"
Балданова Елена # 12 июн 2005	Здравствуйте, Ольга Александровна! У меня к Вам еще парочка вопросов! -Дифференцирование функции нескольких переменных нужно рассматривать в 38 или 39 билете? -Функциональные матрицы в 39 билете должны рассматриваться? -В 44 билете свойства доказывать следует? На сегодня у меня вопросов больше нет! Заранее благодарна!
О.А. # 12 июн 2005	Здравствуйте, Лена. В 38 вопросе подразумевается не только теорема о существовании и единственности неявной функции, заданной системой уравнений, но и правило дифференцирования такой неявной функции. В 39 нужно уметь доказывать достаточное условие независимости функций и знать условия независимости для функциональных матриц. В 44 вопросе нужно лишь перечислить основные свойства двойных интегралов.
Алексей # 12 июн 2005	Здравствуйте, Ольга Александровна. А на консультации 14.06.06 в 12.00 будут рассматриваться наши вопросы или же просто организационные вопросы по экзамену? Также можно узнать критерии оценочной системы на экзамене? В начале мы также, как и в первом семестре будет решать практику, а уже потом теорию?
О.А. # 12 июн 2005	Здравствуйте, Алексей. Все традиции сохраняются, кроме возможности многократно заглядывать в тетрадь с лекциями. Как и в прошлом семестре на консультации я перечислю темы,на которые следует обратить внимание при подготовке к практике.
Ваш ответ:	Чтобы написать сообщение, необходимо войти или зарегистрироваться

Страницы: 1 2 3 4 5 6 7