Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Дмитрий
#
19 янв 2007 |
|
|
О.А.
#
19 янв 2007 |
|
|
Дмитрий
#
19 янв 2007 |
|
|
О.А.
#
19 янв 2007 |
|
|
Дмитрий
#
19 янв 2007 |
|
|
О.А.
#
19 янв 2007 |
|
|
Наталия
#
8 фев 2008 |
|
|
О.А.
#
8 фев 2008 |
|
|
Наталия
#
8 фев 2008 |
|
|
Женя
#
18 янв 2009 |
|
|
О.А.
#
18 янв 2009 |
|
|
Женя
#
19 янв 2009 |
|
|
О.А.
#
19 янв 2009 |
|
|
НАДЕЖДА
#
21 фев 2009 |
|
|
О.А.
#
22 фев 2009 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
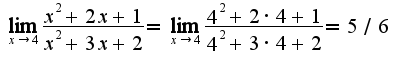 2)Из тригонометрии известно равенство
2)Из тригонометрии известно равенство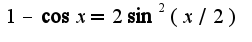 Для решения надо использовать асимптотическое равенство:
Для решения надо использовать асимптотическое равенство: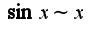 при
при 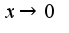
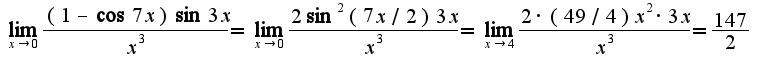
 , в данном примере на
, в данном примере на 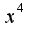 , поэтому предел равен отношению коэффициентов при старших степенях числителя и знаменателя, т.е. 1/2.
2)у меня опечатка
, поэтому предел равен отношению коэффициентов при старших степенях числителя и знаменателя, т.е. 1/2.
2)у меня опечатка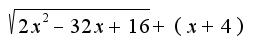 и найти предел,
и найти предел, 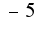
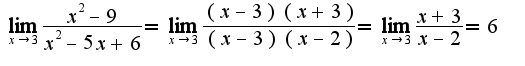
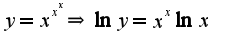
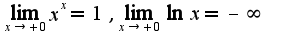 сл-но, предел равен
сл-но, предел равен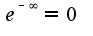
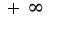 или
или