Поиск
| Автор | Сообщение |
|---|---|
|
Anton
#
26 дек 2007 |
|
|
О.А.
#
26 дек 2007 |
|
|
Anton
#
26 дек 2007 |
|
|
Anton
#
26 дек 2007 |
|
|
О.А.
#
26 дек 2007 |
|
|
Anton
#
26 дек 2007 |
|
|
Anton
#
3 янв 2008 |
|
|
О.А.
#
3 янв 2008 |
|
|
LilOo
#
15 янв 2008 |
|
|
О.А.
#
15 янв 2008 |
|
|
LilOo
#
16 янв 2008 |
|
|
О.А.
#
17 янв 2008 |
|
|
DilER
#
7 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
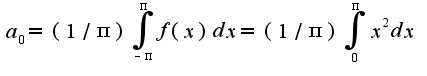
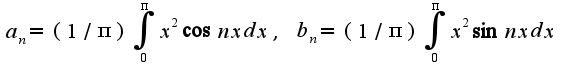
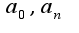 найдены верно,
найдены верно,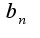 -неверно, кроме того, надо учесть
-неверно, кроме того, надо учесть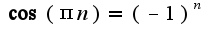
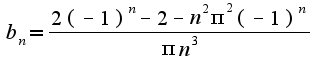
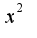 надо подставить данные функции
надо подставить данные функции
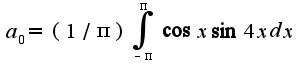
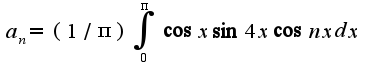
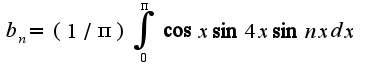 А разве какие-то из элементов не должны быть равны нулю? И как влияет четность\нечетность функций на значения элементов?
спасибо.
А разве какие-то из элементов не должны быть равны нулю? И как влияет четность\нечетность функций на значения элементов?
спасибо.
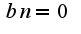 , если нечетная, то
, если нечетная, то