| Автор | Сообщение |
|---|---|
|
Ольга Шабалина
#
3 янв 2005 |
|
|
О.А.
#
3 янв 2005 |
|
|
Алексей
#
5 янв 2005 |
|
|
О.А.
#
5 янв 2005 |
|
|
Марченкова Анастасия
#
7 янв 2005 |
|
|
Шиняева Катя
#
7 янв 2005 |
|
|
О.А.
#
7 янв 2005 |
|
|
Шиняева Катя
#
7 янв 2005 |
|
|
О.А.
#
7 янв 2005 |
|
|
Марченкова Анастасия
#
7 янв 2005 |
|
|
Шиняева Катя
#
8 янв 2005 |
|
|
О.А.
#
9 янв 2005 |
|
|
Алексей
#
10 янв 2005 |
|
|
Шиняева Катя
#
10 янв 2005 |
|
|
О.А.
#
10 янв 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
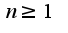 -нечетное число, и функция
-нечетное число, и функция 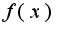 имеет производную порядка
имеет производную порядка 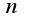 в окрестности точки
в окрестности точки 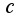 и производную порядка
и производную порядка 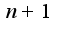 в точке
в точке 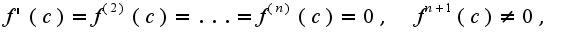 то функция имеет в точке
то функция имеет в точке 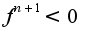 -локальный максимум, при
-локальный максимум, при 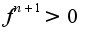 - минимум.
3)Третье достаточное условие существования точек перегиба.
Пусть
- минимум.
3)Третье достаточное условие существования точек перегиба.
Пусть 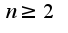 -четное число, и функция
-четное число, и функция 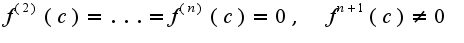 , то график функции имеет перегиб в точке (с,f(с)) .
, то график функции имеет перегиб в точке (с,f(с)) .